MAST
Public Member Functions | Public Attributes | Protected Member Functions | Protected Attributes | List of all members
MAST::ContinuationSolverBase Class Referenceabstract

the equation set is: 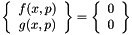$ \left\{ \begin{array}{c} f(x, p) \\ g(x, p) \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ 0 \end{array} \right\} $ the N-R updates are calculated such that

\[ \left[ \begin{array}{cc} df/dx & df/dp \\ dg/dx & dg/dp \end{array}\right] \left\{ \begin{array}{c} dx \\ dp \end{array} \right\} = - \left\{ \begin{array}{c} f(x0, p0) \\ g(x0, p0) \end{array} \right\} \]

This equation is solved using Schur-factorization so that the disciplinary linear solver can be used. More...

#include <continuation_solver_base.h>

Inheritance diagram for MAST::ContinuationSolverBase:
Inheritance graph
[legend]
Collaboration diagram for MAST::ContinuationSolverBase:
Collaboration graph
[legend]

Public Member Functions

 ContinuationSolverBase ()
 
virtual ~ContinuationSolverBase ()
 
void set_assembly_and_load_parameter (MAST::AssemblyElemOperations &elem_ops, MAST::AssemblyBase &assembly, MAST::Parameter &p)
 sets the assembly object for this solver More...
 
void clear_assembly_and_load_parameters ()
 clears the assembly object from this solver More...
 
virtual void initialize (Real dp)=0
 initializes the data structure based on initial load step dp. More...
 
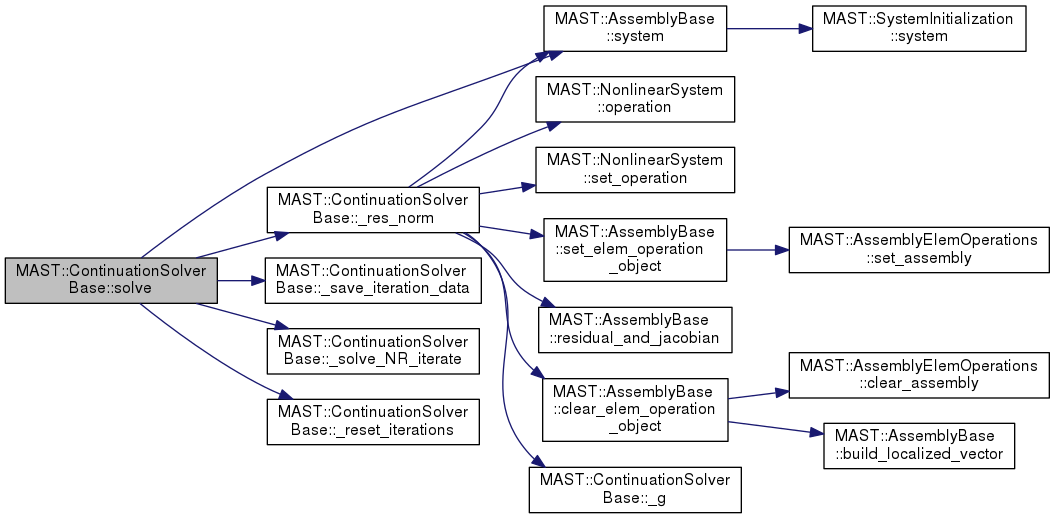
virtual void solve ()
 solves for the next load step More...
 

Public Attributes

unsigned int max_it
 Maximum number of Newton-Raphson iterations for the solver. More...
 
Real abs_tol
 Absolute tolerance for the solver. More...
 
Real rel_tol
 Relative tolerance for the solver. More...
 
Real arc_length
 arc length that the solver is required to satisfy for the update. More...
 
Real min_step
 minimum step size allowed with adaptivity More...
 
Real max_step
 maximum step size allowed with adaptivity More...
 
Real step_size_change_exponent
 exponent used in step size update. More...
 
unsigned int step_desired_iters
 desired N-R iterations per load-step. More...
 
bool schur_factorization
 flag to use Schur-factorizaiton (default) or monolithic solver More...
 

Protected Member Functions

virtual void _solve_NR_iterate (libMesh::NumericVector< Real > &X, MAST::Parameter &p)=0
 
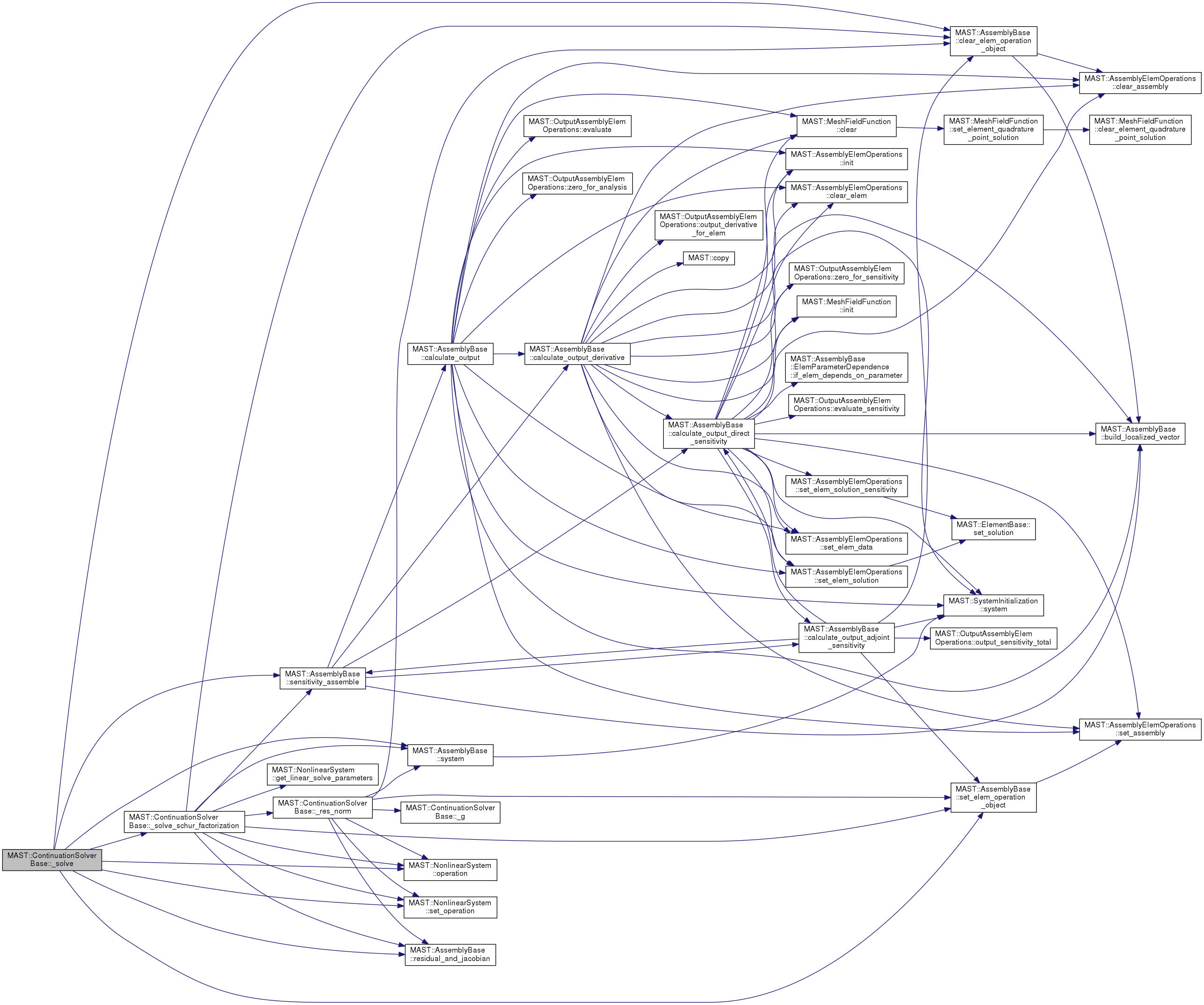
void _solve (const libMesh::NumericVector< Real > &X, const MAST::Parameter &p, libMesh::NumericVector< Real > &f, bool update_f, libMesh::NumericVector< Real > &dfdp, bool update_dfdp, const libMesh::NumericVector< Real > &dgdX, const Real dgdp, const Real g, libMesh::NumericVector< Real > &dX, Real &dp)
 solves for the linear system of equation as a monolithic system

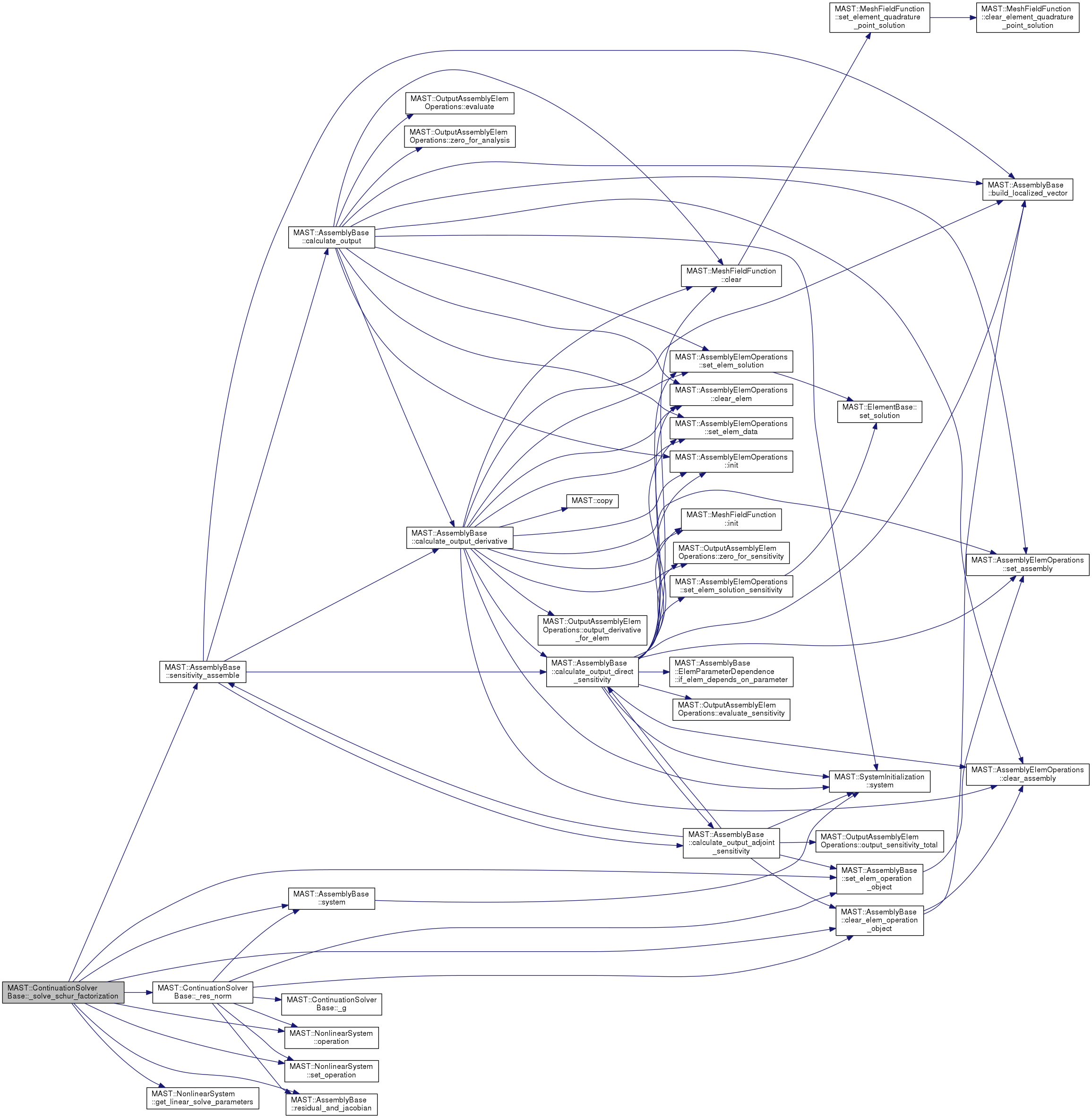
\[ \left[ \begin{array}{cc} df/dx & df/dp \\ dg/dx & dg/dp \end{array}\right] \left\{ \begin{array}{c} dx \\ dp \end{array} \right\} = - \left\{ \begin{array}{c} f \\ g \end{array} \right\} \]

dX and dp are returned from the solution More...

 
void _solve_schur_factorization (const libMesh::NumericVector< Real > &X, const MAST::Parameter &p, libMesh::SparseMatrix< Real > &jac, bool update_jac, libMesh::NumericVector< Real > &f, bool update_f, libMesh::NumericVector< Real > &dfdp, bool update_dfdp, libMesh::NumericVector< Real > &dXdp, bool update_dXdp, const libMesh::NumericVector< Real > &dgdX, const Real dgdp, const Real g, libMesh::NumericVector< Real > &dX, Real &dp)
 solves for the linear system of equation using Schur factorization. More...
 
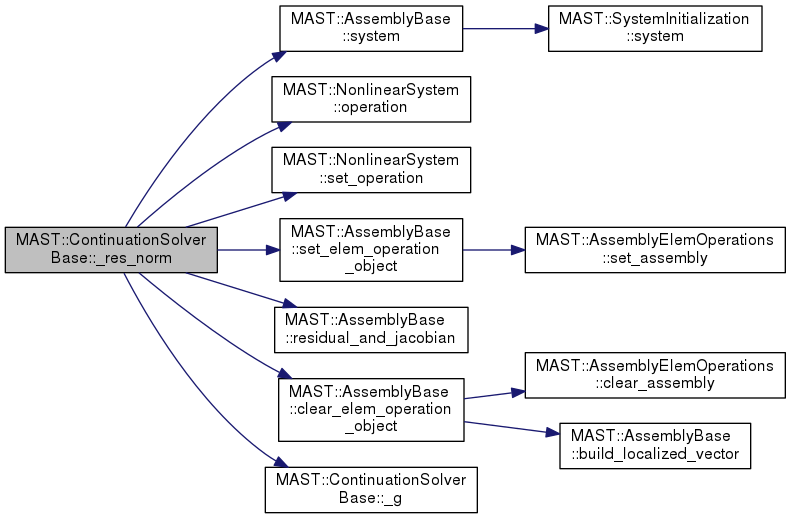
Real _res_norm (const libMesh::NumericVector< Real > &X, const MAST::Parameter &p)
 
virtual Real _g (const libMesh::NumericVector< Real > &X, const MAST::Parameter &p)=0
 
virtual void _save_iteration_data ()=0
 method saves any data for possible resuse if the solution step is restarted More...
 
virtual void _reset_iterations ()=0
 method resets any data if a soltion step is restarted More...
 

Protected Attributes

bool _initialized
 
MAST::AssemblyElemOperations * _elem_ops
 
MAST::AssemblyBase * _assembly
 
MAST::Parameter * _p
 
Real _p0
 
Real _X_scale
 
Real _p_scale
 
std::unique_ptr< libMesh::NumericVector< Real > > _X0
 

Detailed Description

the equation set is: 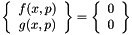$ \left\{ \begin{array}{c} f(x, p) \\ g(x, p) \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ 0 \end{array} \right\} $ the N-R updates are calculated such that

\[ \left[ \begin{array}{cc} df/dx & df/dp \\ dg/dx & dg/dp \end{array}\right] \left\{ \begin{array}{c} dx \\ dp \end{array} \right\} = - \left\{ \begin{array}{c} f(x0, p0) \\ g(x0, p0) \end{array} \right\} \]

This equation is solved using Schur-factorization so that the disciplinary linear solver can be used.

Definition at line 53 of file continuation_solver_base.h.

Constructor & Destructor Documentation

MAST::ContinuationSolverBase::ContinuationSolverBase ( )

Definition at line 37 of file continuation_solver_base.cpp.

MAST::ContinuationSolverBase::~ContinuationSolverBase ( )
virtual

Definition at line 59 of file continuation_solver_base.cpp.

Here is the call graph for this function:

Member Function Documentation

virtual Real MAST::ContinuationSolverBase::_g ( const libMesh::NumericVector< Real > &  X,
const MAST::Parameter &  p 
)
protectedpure virtual

Implemented in MAST::PseudoArclengthContinuationSolver, and MAST::ArclengthContinuationSolver.

Here is the caller graph for this function:

Real MAST::ContinuationSolverBase::_res_norm ( const libMesh::NumericVector< Real > &  X,
const MAST::Parameter &  p 
)
protected
Returns
the norm of residual at given solution and load parameter.

Definition at line 570 of file continuation_solver_base.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

virtual void MAST::ContinuationSolverBase::_reset_iterations ( )
protectedpure virtual

method resets any data if a soltion step is restarted

Implemented in MAST::PseudoArclengthContinuationSolver, and MAST::ArclengthContinuationSolver.

Here is the caller graph for this function:

virtual void MAST::ContinuationSolverBase::_save_iteration_data ( )
protectedpure virtual

method saves any data for possible resuse if the solution step is restarted

Implemented in MAST::PseudoArclengthContinuationSolver, and MAST::ArclengthContinuationSolver.

Here is the caller graph for this function:

void MAST::ContinuationSolverBase::_solve ( const libMesh::NumericVector< Real > &  X,
const MAST::Parameter &  p,
libMesh::NumericVector< Real > &  f,
bool  update_f,
libMesh::NumericVector< Real > &  dfdp,
bool  update_dfdp,
const libMesh::NumericVector< Real > &  dgdX,
const Real  dgdp,
const Real  g,
libMesh::NumericVector< Real > &  dX,
Real &  dp 
)
protected

solves for the linear system of equation as a monolithic system

\[ \left[ \begin{array}{cc} df/dx & df/dp \\ dg/dx & dg/dp \end{array}\right] \left\{ \begin{array}{c} dx \\ dp \end{array} \right\} = - \left\{ \begin{array}{c} f \\ g \end{array} \right\} \]

dX and dp are returned from the solution

Definition at line 184 of file continuation_solver_base.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

virtual void MAST::ContinuationSolverBase::_solve_NR_iterate ( libMesh::NumericVector< Real > &  X,
MAST::Parameter &  p 
)
protectedpure virtual

Implemented in MAST::PseudoArclengthContinuationSolver, and MAST::ArclengthContinuationSolver.

Here is the caller graph for this function:

void MAST::ContinuationSolverBase::_solve_schur_factorization ( const libMesh::NumericVector< Real > &  X,
const MAST::Parameter &  p,
libMesh::SparseMatrix< Real > &  jac,
bool  update_jac,
libMesh::NumericVector< Real > &  f,
bool  update_f,
libMesh::NumericVector< Real > &  dfdp,
bool  update_dfdp,
libMesh::NumericVector< Real > &  dXdp,
bool  update_dXdp,
const libMesh::NumericVector< Real > &  dgdX,
const Real  dgdp,
const Real  g,
libMesh::NumericVector< Real > &  dX,
Real &  dp 
)
protected

solves for the linear system of equation using Schur factorization.

\[ \left[ \begin{array}{cc} df/dx & df/dp \\ dg/dx & dg/dp \end{array}\right] \left\{ \begin{array}{c} dx \\ dp \end{array} \right\} = - \left\{ \begin{array}{c} f \\ g \end{array} \right\} \]

dX and dp are returned from the solution

Definition at line 421 of file continuation_solver_base.cpp.

Here is the call graph for this function:

Here is the caller graph for this function:

void MAST::ContinuationSolverBase::clear_assembly_and_load_parameters ( )

clears the assembly object from this solver

Definition at line 82 of file continuation_solver_base.cpp.

virtual void MAST::ContinuationSolverBase::initialize ( Real  dp)
pure virtual

initializes the data structure based on initial load step dp.

must be called before solve().

Implemented in MAST::PseudoArclengthContinuationSolver, and MAST::ArclengthContinuationSolver.

void MAST::ContinuationSolverBase::set_assembly_and_load_parameter ( MAST::AssemblyElemOperations &  elem_ops,
MAST::AssemblyBase &  assembly,
MAST::Parameter &  p 
)

sets the assembly object for this solver

Definition at line 67 of file continuation_solver_base.cpp.

Here is the caller graph for this function:

void MAST::ContinuationSolverBase::solve ( )
virtual

solves for the next load step

Definition at line 93 of file continuation_solver_base.cpp.

Here is the call graph for this function:

Member Data Documentation

MAST::AssemblyBase* MAST::ContinuationSolverBase::_assembly
protected

Definition at line 224 of file continuation_solver_base.h.

MAST::AssemblyElemOperations* MAST::ContinuationSolverBase::_elem_ops
protected

Definition at line 223 of file continuation_solver_base.h.

bool MAST::ContinuationSolverBase::_initialized
protected

Definition at line 221 of file continuation_solver_base.h.

MAST::Parameter* MAST::ContinuationSolverBase::_p
protected

Definition at line 225 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::_p0
protected

Definition at line 228 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::_p_scale
protected

Definition at line 228 of file continuation_solver_base.h.

std::unique_ptr<libMesh::NumericVector<Real> > MAST::ContinuationSolverBase::_X0
protected

Definition at line 233 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::_X_scale
protected

Definition at line 228 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::abs_tol

Absolute tolerance for the solver.

Default is 1.e-8;

Definition at line 97 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::arc_length

arc length that the solver is required to satisfy for the update.

Definition at line 109 of file continuation_solver_base.h.

unsigned int MAST::ContinuationSolverBase::max_it

Maximum number of Newton-Raphson iterations for the solver.

Default is 20.

Definition at line 91 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::max_step

maximum step size allowed with adaptivity

Definition at line 121 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::min_step

minimum step size allowed with adaptivity

Definition at line 115 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::rel_tol

Relative tolerance for the solver.

Default is 1.e-8;

Definition at line 103 of file continuation_solver_base.h.

bool MAST::ContinuationSolverBase::schur_factorization

flag to use Schur-factorizaiton (default) or monolithic solver

Definition at line 141 of file continuation_solver_base.h.

unsigned int MAST::ContinuationSolverBase::step_desired_iters

desired N-R iterations per load-step.

Step-size is chanegd if actual number of N-R iterates is different from this value using the expression 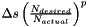$ \Delta s \left(\frac{N_{desired}}{N_{actual}}\right)^p $, where, p is the exponent.

Definition at line 136 of file continuation_solver_base.h.

Real MAST::ContinuationSolverBase::step_size_change_exponent

exponent used in step size update.

Definition at line 127 of file continuation_solver_base.h.

The documentation for this class was generated from the following files: