|
MAST
|
|
MAST
|
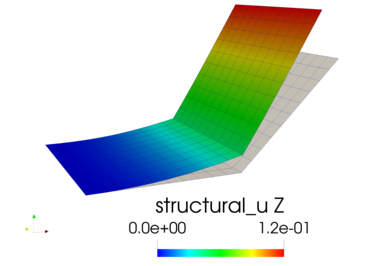
This example solves a cantilever rectangular plate with a uniformly distributed load on the top of the plate.
An inclined section is created as a separate mesh and connected to the plate using tie constraints at the shared edge.
For direct solver, run with options: -ksp_type preonly -pc_type lu
This function initializes the mesh data stucture.
A square 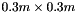 mesh is created with
mesh is created with QUAD4 elements.
The mesh generation tools from libMesh are used to initialize this section of the mesh. A 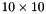 mesh of QUAD4 elements is used for discretization.
mesh of QUAD4 elements is used for discretization.
Next, a section of the same dimension and mesh density is created and added to the mesh object. This section is attached to the right side of the cantilever section (created above) using kinematic constraints. The section is inclined at a 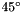 angle.
angle.

add new nodes
add new node to the map so that we will be able to use it during element creation below
modify the coordinates to include the incline.
add new nodes
add new elements
set nodes
set subdomain ID to 1
set boundary IDs
add the boundary tags to the panel mesh
the boundaries are indentified using the following tags.
Initialize libMesh library.
A replicated mesh is used, which will store the entire mesh on all elements.
Initialize the mesh using the function defined above.
Create EquationSystems object, which is a container for multiple systems of equations that are defined on a given mesh.
Add system of type MAST::NonlinearSystem (which wraps libMesh::NonlinearImplicitSystem) to the EquationSystems container. We name the system "structural" and also get a reference to the system so we can easily reference it later.
Create a finite element type for the system. Here we use first order Lagrangian-type finite elements.
Initialize the system to the correct set of variables for a structural analysis. In libMesh this is analogous to adding variables (each with specific finite element type/order to the system for a particular system of equations.
Initialize a new structural discipline using equation_systems.
Create and add boundary conditions to the structural system. A Dirichlet BC adds fixed displacement BCs. Here we use the side boundary ID numbering created by the libMesh generator to clamp the edge of the mesh along x=0.0. We apply the BC to all variables on each node in the subdomain ID 0, which clamps this edge.
Initialize the equation system since we now know the size of our system matrices (based on mesh, element type, variables in the structural_system) as well as the setup of dirichlet boundary conditions. This initialization process is basically a pre-processing step to preallocate storage and spread it across processors.
The tie constraints are added through the DofConstraintRow functionality in libMesh. Here, constraint equations are specified between degrees-of-freedom (DoFs). The first step in the coupling is identified through a geometric search which identifies the nodes on the respective boundaries of master and slave mesh that need to be coupled with each other. Here, the right boundary (boundary id 1) of the cantilevered plate is connected to the left boundary (boundary id 7) of the unconnected domain. Once the nodes have been identified, the next step is to identify the constraint equations that will define the dependence of the slave nodes on the master nodes. This is done by the MeshCouplingBase class. The constraint equations are then provided to libMesh through this ad-hoc class Constr below.
The MeshCouplingBase class will used to couple the boudnary ID 7 as the slave to the boundary ID 1 as the master. A geometric search will be used to identify node couplings within a circular radius of 0.005 m.
This call will lead to a master-slave boundary-to-boundary coupling. This can be uncommented and the next boundary-to-subdomain call can be commented to enable this call. mesh_coupling.add_master_and_slave_boundary_coupling(1, 7, .005);
the mesh can also be coupled using slave-boundary to master-subdomain coupling.
The KinematicCoupling class uses the search results to create the kinematic constraints (or tie-constraints) for libMesh::DofMap
This class will is provided to libMesh::System and it will be called by libMesh when the system is initialized.
This will initialize the DoFs, Dirichlet Constraints and kinematic constraints.
Create parameters.
Create ConstantFieldFunctions used to spread parameters throughout the model.
Initialize load. The same pressure is applied to both sub-domains 1 and 2.
Create the material property card ("card" is NASTRAN lingo) and the relevant parameters to it. An isotropic material needs elastic modulus (E) and Poisson ratio (nu) to describe its behavior.
Create the section property card. Attach all property values.
Attach material to the card.
Initialize the specify the subdomain in the mesh that it applies to.
Create nonlinear assembly object and set the discipline and structural_system. Create reference to system.
Zero the solution before solving.
post-process the stress for plotting. This is done through the output and stress assembly classes.
Following is a the displacement contour of the panel with the undeformed mesh plotted for reference. The displacement continuity at the interface is properly enforced.